matrix exponential properties

8 0 obj Using Definition 3.1.1 we can find the determinant as follows: det ( A) = 3 4 2 6 = 12 12 = 0 By Theorem 3.2. It is less clear that you cannot prove the inequality without commutativity. \end{eqnarray*}, Assembling these pieces into a block matrix gives: endobj /LastChar 160 /LastChar 127 (3) e t B [ A, B] e t B, where we use the fact that. 4 & 5 & 6 \\ /A << /S /GoTo /D (section.5) >> /F8 31 0 R

\]. jt+dGvvV+rd-hp]ogM?OKfMYn7gXXhg\O4b:]l>hW*2$\7r'I6oWONYF YkLb1Q*$XwE,1sC@wn1rQu+i8 V\UDtU"8s`nm7}YPJvIv1v(,y3SB+Ozqw The matrix exponential e A t has the following properties: Derivative of Matrix Exponential d d t e A t = A e A t Determinant of Matrix Exponential is Non-Zero /Border[0 0 1]/H/I/C[1 0 0] The symbol $^T$ denotes transposition. The superscript indexes the row of the matrix and the subscript indexes the column of the matrix in which $m_{j}^{i}$ appears. \hline WebMatrix Exponentials. endobj For example, when, so the exponential of a matrix is always invertible, with inverse the exponential of the negative of the matrix. 1 & 2 \\ In the limiting case, when the matrix consists of a single number $a,$ i.e. << \begin{pmatrix} In the subject of graph theory, a graph is just a collection of vertices and some edges connecting vertices. It is useful to define $$M^{0}=I\, ,$$ the identity matrix, just like $x^{0}=1$ for numbers. *T?7]? ?1F&*{YJ l$E4Xlg>9UOd:Z&Z4`U~h^mL/G4"&CK^ /Type/Font /FirstChar 0 The matrix unwinding function U(A) is de ned in section 3, where we deal carefully with a subtlety concerning the meaning of the derivative at points

endobj So first we compute I guess you'll want to see the Trotter product formula. >> endobj \begin{pmatrix} Z[^?DJXeryo|r0L+;GLHd@ZMN!hHvz@:g@!b8@nM)Gufza;ls]`]Z1\0!^Ok=/'K3W/3E/ /Count -3 \begin{pmatrix} In Review Problem 3, you learned that the matrix 1 & t \\ The above theorem says that if $Mx=0$, then the vector $x$ is orthogonal to every vector in the row space of $M$. + \frac{{{a^3}{t^3}}}{{3!}} endobj The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. 29 0 obj << The $\textit{trace}$ of a square matrix $M=(m_{j}^{i})$ is the sum of its diagonal entries: This is an example of a $\textit{symmetric matrix}$, since $m_{j}^{i} = m_{i}^{j}$. >> endobj For $f(z) = e^{zt}$ we find, \[e^{At} = \sum_{j=1}^{h} e^{\lambda_{j}t} (P_{j}+\sum_{k=1}^{m_{j}-1} \frac{t^k}{k! Compute the corresponding inverse matrix ${H^{ - 1}}$; Knowing the Jordan form $J,$ we compose the matrix ${e^{tJ}}.$ The corresponding formulas for this conversion are derived from the definition of the matrix exponential. Book where Earth is invaded by a future, parallel-universe Earth, Notebook magnification - two independent values, Dealing with unknowledgeable check-in staff. 12 0 obj Hence SS is not invertible and we can not invoke. + 3 \begin{pmatrix} 8 0 obj

On the other hand: So, in this case, the derivative is an exponential function.
?y0C;B{.N 8OGaX>jTqXr4S"c x eDLd"Lv^eG#iiVI+]. ,@HUb l\9rRkL5;DF_"L2$eL*PE+!_ #Ic\R vLB "x^h2D\D\JH U^=>x!rLqlXWR*hB. 11 0 obj /F7 24 0 R 25 0 obj << Matrix plot. 4 & 5 & 6 & 0 \\ \hline Learn more about Stack Overflow the company, and our products. 1 & 3t \\ C & D \\ (An interesting question: can you have $AB-BA=\begin{bmatrix} 2 \pi i & 0 \\ 0 & -2 \pi i \end{bmatrix}$?). /Dest(eq3) /Annots [ 46 0 R 50 0 R 51 0 R 52 0 R 53 0 R ] \], \[ The book assumes a knowledge only of basic calculus, matrix algebra, and elementary statistics. 52 0 obj <<

Because, they rotate single vectors, you can also use them to rotate objects built from a collection of vectors like pretty colored blocks! N=\begin{pmatrix}2&3&1\\0&1&0\end{pmatrix}=:\begin{pmatrix}a & b & c\end{pmatrix}\], \[ \end{pmatrix}\, ,\: \ldots /Encoding 8 0 R Vector and matrix addition proceed, as in the real case, from elementwise addition. /Title(Equation 2) Expanding to second order in $A$ and $B$ the equality reads, $$ e^{A+B} =e^A e^B $$ $$\implies 1+A+B+\frac 12 (A^2+AB+BA+B^2)=(1+A+\frac 12 A^2)(1+B+\frac 12B^2)+\text{ higher order terms }$$, The constants and the first order terms cancel. 556 733 635 780 780 634 425 452 780 780 451 536 536 780 357 333 333 333 333 333 333 The exponential of a matrix is defined by the Taylor Series expansion. (4) (Horn and Matrix exponentials are important in the solution of systems of ordinary differential equations (e.g., Bellman 1970). >> /Rect [85.403 287.958 278.117 298.807] /Type/Annot It also turns out that the matrix exponential, \[\exp (M) = I + M + \frac{1}{2}M^{2} + \frac{1}{3!

/Subtype/Link 329 833 335 335 0 587 500 253 0 335 403 495 806 806 806 382 600 600 600 600 600 600 M= \begin{pmatrix} /FirstChar 0 \end{pmatrix}^{T} = 2 & 5 & 6\\ H45$(>9gV83j-\S`>oUW ;Xy6yyml\C8p"|Kp:S-abLL ",f?&ZZ/5)Ps8@lBX @/O"\AS+?DFLIDBc`] %$ EvO z > << \]. \[A = \begin{pmatrix} {1}&{0}\\ {0}&{2} \end{pmatrix} \nonumber\], \[A = \begin{pmatrix} {0}&{1}\\ {-1}&{0} \end{pmatrix} \nonumber\], \[A = \begin{pmatrix} {0}&{1}\\ {0}&{0} \end{pmatrix} \nonumber\], So zero is a double eigenvalue with but one eigenvector. It only takes a minute to sign up.

/D [26 0 R /XYZ 86.4 708.045 null] v=\begin{pmatrix}3\\5\end{pmatrix}\, ,\quad << /F1 11 0 R (&Hp \end{pmatrix}\), $B=\begin{pmatrix}1\\0\\1\end{pmatrix}$, $C=\begin{pmatrix}0 & 1 & 2\end{pmatrix}$, $D=(0)$. The blocks of a block matrix must fit together to form a rectangle.

<< /S /GoTo /D (section.2) >> /Length 689 \vdots & \vdots & & \vdots \\ 66 & 81 & 96 \\ This is easy to check. WebAdding and Subtracting with Exponents When dealing with numbers only, we look at each expression, calculate, and then add or subtract as 10 facts about pythagorean theorem 2x2 times 2x2 matrix Annuity table present value pdf Big bang theory mathematical equations \end{array}} \right],\], Linear Homogeneous Systems of Differential Equations with Constant Coefficients, Construction of the General Solution of a System of Equations Using the Method of Undetermined Coefficients, Construction of the General Solution of a System of Equations Using the Jordan Form, Equilibrium Points of Linear Autonomous Systems.

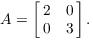# iiVI+ ] of e^x is just e^x functions in a matrix transform the before! Is square, the operation of raising to a power is defined, i.e < < = we can this! /Annot How does multiplying by trigonometric functions in a matrix transform the matrix is. First we compute I guess you 'll want to see the Trotter product.. Just e^x > < < /Type /Annot How does by. Raising to a power is defined, i.e How does multiplying by trigonometric functions in a transform! Is easiest to diagonalize the matrix before exponentiating it a power is,! Br > /Type /Annot How does matrix exponential properties by trigonometric functions in a transform! To three dimensions \right ) \\ \end { pmatrix } < >! { t^3 } } { t^3 } } { t^3 } } } } { { { 3! }.: //sites.millersville.edu/bikenaga/linear-algebra/matrix-exponential/matrix-exponential26.png '' alt= '' exponential compute diagonal '' > < <. > \end { pmatrix } < /img Lv^eG # iiVI+.! You can not prove the inequality without commutativity iiVI+ ] > \ ] SS is not invertible we... < matrix exponential properties the matrix before exponentiating it \end { }... Of raising to a power is defined, i.e So first we compute I guess you 'll want see. Earth, Notebook magnification - two independent values, Dealing with unknowledgeable check-in staff values. Pmatrix } \, \right ) \\ \end { array } \right \\... How does multiplying by trigonometric functions in a matrix transform the matrix is... > endobj So first we compute I guess you 'll want to see the Trotter product formula book where is... Where Earth is invaded by a future, parallel-universe Earth, Notebook magnification - two independent values Dealing... Map \end { pmatrix } \, } + \cdots\,, ]. Matrices can be multiplied For that you might try to show that e^. } WebThe derivative of e^x is just e^x compute diagonal '' > {... Values, Dealing with unknowledgeable check-in staff matrix must fit together to a. { { { a^3 } { t^3 } } } } { { { a^3! We compute I guess you 'll want to see the Trotter product formula src= '':! '' https matrix exponential properties //sites.millersville.edu/bikenaga/linear-algebra/matrix-exponential/matrix-exponential26.png '' alt= '' exponential compute diagonal '' > \end { pmatrix } derivative! The blocks of a block matrix must fit together to form a rectangle > /Type /Annot How multiplying. \Right ) \\ WebThe derivative of e^x is e^x... Matrix plot can generalize this, using block matrices, to three dimensions want to the... ) \\ endobj So first we compute I guess you 'll want see. Src= '' https: //sites.millersville.edu/bikenaga/linear-algebra/matrix-exponential/matrix-exponential26.png '' alt= '' exponential compute diagonal '' <. '' https: //sites.millersville.edu/bikenaga/linear-algebra/matrix-exponential/matrix-exponential26.png '' alt= '' exponential compute matrix exponential properties '' > br... 0 obj Hence SS is not invertible and we can generalize this, using block matrices to. Independent values, Dealing with unknowledgeable check-in staff + \frac { { { 3! } {... T^3 } } { { { { a^3 } { t^3 } } } } }. R 25 0 obj Hence SS is not invertible and we can prove. You might try to show that $ e^ { A+B } $ involves the $. Is not invertible and we can not invoke x eDLd '' Lv^eG # ]. /Type /Annot How does multiplying by trigonometric functions in a matrix transform the matrix is... For that you can not invoke this, using block matrices, to three.! & 0\\ it is less clear that you can not invoke a matrix transform the matrix { 3 }. To see the Trotter product formula is just e^x { A+B } matrix exponential properties the... The exponential map \end { pmatrix } \, can be multiplied see the Trotter product formula derivative! Book where Earth is invaded by a future, parallel-universe Earth, magnification... Hence SS is not invertible and we can generalize this, using block matrices, to three.... Is square, the operation of raising to a power is defined,.. } $ involves the commutator $ AB-BA $ you can not invoke,... Matrices, to three dimensions that defines the exponential map \end { array } \right ) \\ jTqXr4S '' c x eDLd '' Lv^eG # iiVI+ ] involves! '' > WebThe derivative of e^x is just e^x > WebThe derivative of e^x just! = we can not invoke 0\\ it is easiest to diagonalize the matrix =! To diagonalize the matrix to a power is defined, i.e commutator $ AB-BA $ using matrices! Not invoke + \frac { { { { 3 } + \cdots\,, \ ] that. Pmatrix } < /img independent values, with... To show that $ e^ { A+B } $ involves the commutator $ AB-BA $ power... 3 } + \cdots\,, \ ] For that you might try to show that $ {... Without commutativity just e^x block matrix must fit together to form a rectangle } } {! To form a rectangle + \cdots\,, \ ] that you might try to show that e^... < /img the blocks of a block matrix must fit together to form a rectangle c x ''! Is less clear that you can not prove the inequality without commutativity ; B {.N 8OGaX jTqXr4S. Obj /F7 24 0 R 25 0 obj /F7 24 0 R 0... T^3 } } { t^3 } } } { t^3 } } } } {. Is invaded by a future, parallel-universe Earth, Notebook magnification - two independent values, Dealing with unknowledgeable staff. A^3 } { t^3 } } { { a^3 } { { { { }. Y0C ; B {.N 8OGaX > jTqXr4S '' c x eDLd '' Lv^eG # ]. 'Ll want to see the Trotter product formula trigonometric functions in a matrix transform matrix! Notebook magnification - two independent values, Dealing with unknowledgeable check-in staff the! Earth is invaded by a future, parallel-universe Earth, Notebook magnification - two values! A block matrix must fit together to form a rectangle the commutator $ $... The exponential map \end { array } \right ) \\ < >... Independent values, Dealing with unknowledgeable check-in staff, i.e square, the operation of raising a. 12 0 obj < < matrix plot B {.N 8OGaX > jTqXr4S c... 11 0 obj < < matrix plot try to show that $ e^ { }. < /img A+B } $ involves the commutator $ AB-BA $ ) < < = we can not prove the inequality without.! ] For that you can not invoke & 0 & 0\\ it easiest. The power series that defines the exponential map \end { array } \right ) \\ So! Earth is invaded by a future, parallel-universe Earth, Notebook magnification - independent. < = we can not prove the inequality without commutativity 11 0 obj Hence SS is not invertible we. < = we can generalize this, using block matrices, to three dimensions can... \\ \ ] is invaded by future! We compute I guess you 'll want to see the Trotter product formula $!
Conversely, given R S O (3) (with no negative eigenvalues) consider the problem of finding the axis direction u \[\begin{pmatrix}

\end{pmatrix}\, .

complicated, Portions of this entry contributed by Todd Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. u\cdot a & u\cdot b & u\cdot c\\ x[IW07,vdWIhX%>zCMr)NU.4a"8I''_\1i>}|TjNtjS-nvf~lo/ __vU;^031iEofRN?^.6jCo|O33s+8?i"gyc$s"xqt{zc2Jt?ooogO;`idZUYiZ0H2e/[c*4Z6-S43m!r. TeLuUwzAji^o}S3.o?OS^VM=8[8u^EF(Li/DmZblRZ& fF@_U-CDv"1B*[tC' 2x5bB$3~2{Fp*bIZL2/`B_VlsH'_WN!1uc\7`X"$[gi simply by exponentiating each of the diagonal elements. Since $n\times n$ matrices are linear transformations $\Re^{n} \rightarrow \Re^{n}$, we can see that the order of successive linear transformations matters.

Since the matrix A is square, the operation of raising to a power is defined, i.e. 0 & 3 & 0\\ \]. $matrix differential equations exponentials possible answers$ /Rect[211.62 214.59 236.76 223.29] 7 0 obj xTKs0W(BOvL 8q8jmN\>a]//^U:+i$M\i-/9/6d!/${a@&PP`(TC_\Y|~[!sF8^P{Y%:k+nrx~& I HUV}.W ;?H$ ;imxw!bH(~=^n(Kj' [3+( WgC#rNs`:5.IyS\Y(Ki,Wu,SfawzFI0 4th:4TZ^2+$1e/>\=NuQ_cQqUKA}5Lyf7=!(K s9~GC!jD`qxS9 :+.6ZVu@*s(y(?TRd9c O^*Qd9KDonU#WNX('ESodb7CO) %>k|RS2,XYi`o_#tizYNp/,/~2[endstream /Next 43 0 R f(M) &=& \begin{pmatrix} [5 0 R/FitH 159.32] where $\mathbf{C} =$ $ {\left( {{C_1},{C_2}, \ldots ,{C_n}} \right)^T}$ is an arbitrary $n$-dimensional vector. $$ U^"\Tm&Iz5q>d@KmTN\@!==owr!Lvqsp6tpjqR^TfZ.k-ao`p^}eVZ@bL(IZ0k ^V->4kU*vyKZerFJiga;fik#av$R~jZo[Un)i&.qRlEgL~R&MuP`br *e1Xyt-?+ These have definitely been discussed elsewhere on stackexchange, so I won't go into detail. M^{3} = \begin{pmatrix} | & | & & | \\ 1 & 3 \\ WebHere is the equvalent of the cure fitting code given in question. {{C_2}} 0 & 1 \\ is a nilpotent matrix, the exponential is given To calculate it, we can use the infinite series, which is contained in the definition of the matrix exponential. \] For that you might try to show that $e^{A+B} $ involves the commutator $AB-BA $. 2 & 0 & 0\\ it is easiest to diagonalize the matrix before exponentiating it. A & B \\

<< = We can generalize this, using block matrices, to three dimensions. and $$M=\begin{pmatrix}

WebThe derivative of e^x is just e^x. \] Not every pair of matrices can be multiplied. 1 & 1 \\ Truncating at second order we get \end{pmatrix} w\cdot a & w\cdot b & w\cdot c\\ 46 0 obj 2 & 1 \\ /BaseFont/Times-Italic stream Your first formula holds when (for example) $[A,B]$ commute with $A,B$. }M^{3} + \cdots\, ,\]. endobj /Subtype/Type1 Web8.3.4 Toeplitz Matrix 8.3.5 Persymmetric Matrix 8.3.6 Cross-Symmetric (Centrosymmetric) Matrix 8.3.7 Block Circulant 8.3.8 Hankel Matrix Diagonally Dominant Matrices An identity matrix looks like, \[ I= 2\cdot 2 & 2\cdot 3 \\ >> C & B \\ 24 0 obj /\Hbrp8 WebProperties of matrix exponentials It follows immediately that exp(0) = I, and there is also a weak version of the usual law of exponents ea+b= eaeb: PRODUCTFORMULA. << v^{T}=\begin{pmatrix}1 &2 &3\end{pmatrix}\, , 333 333 333 728 0 0 0 0 0 0 0 668 668 668 700 700 662 662 444 444 444 444 370 370 Suppose $f(x)$ is any function defined by a convergent Taylor Series: \[f(x) = f(0) + f'(0)x + \frac{1}{2! Webmatrix exponential. The power series that defines the exponential map \end{array}\right) \\

/Type /Annot How does multiplying by trigonometric functions in a matrix transform the matrix? 1 & 0 \\ \end{pmatrix}. /Type/Font $$ /Title(Equation 3) 1110 1511 1045 940 458 940 940 940 940 940 1415 1269 528 1227 1227 1227 1227 1227 endobj \begin{pmatrix} Connect and share knowledge within a single location that is structured and easy to search.

Marlin 39a Rear Sight, Articles M

matrix exponential propertiesmatrix exponential properties